-

-
Bastides bienvenue :
-
Définition de "Bastide",
- leurs
caractéristiques,
- leurs
Chartes.
- Le
Tracé orthogonal,
-
urbanisme gothique
- la Place,
- la Halle,
-
les Maisons,
- les Cornières un
problème,
- les Andrones,
- L'église
- les Remparts
: avec ou sans.
- Chateau : avec
ou sans
- Puits et
ponts
-
Bastides Modèles (Typologie)
-
Contexte historique.
-
Chronologie Générale
-
Monflanquin bastide type
- .
-
Présentation par :
- Musée des
Bastides,
- Action
pédagogique,
-
La bastide Mystère
- Centre Etude
Bastides,
-
Interreg : Europe Sud
- Bibliographie,
- Cartographie
- Vues
aeriennes
- Glossaire,
-
Toponymie.
- .
-
Bastides
Répertoire
- par
départements,
- par
fondateurs
- et global
- .
-
L'orthogonalité :
- en Europe,
- hors d'Europe,
- dans l'Antiquité,
- dans la
théorie.
- dans la
peinture.
- .
-
sur sites
internet
- par bastide :
-
A à M
-
N à V
- par Thèmes
-
carte interactive
-
-
Annexes sur :
-
les villes en étoile,
-
les "circulades",
-
Sauvetés et castelnaus
-
-
Recherche d'une vue
aérienne de ville sur "google earth"
-
*Lecteurs*
-
|
|
|
Odo Georges |
|
Site traduit en : |
|
|
|
|

 |
-
 |
| |
- Plan
- orthogonal.
-
- I/ Plan
Théorique :
-
- La bastide est essentiellement une ville neuve, décidée et réalisée.
Dés lors le fondateur est à même de projeter le plan de sa
réalisation.
- Retenu par Viollet le Duc, le plan
de Monpazier est devenu au XIX° Siècle le plan théorisé des bastides.
On y retrouve la conception de la ville idéale selon Eiximentis au XIV°
siècle, ville au plan orthogonal.
- Cette approche de l'étude des
bastides a été revue avec les études de Lavedan et Hugueney.
- En fait une quinzaine de bastides
présentent une régularité du tracé aussi stricte : Bretenoux, Saint
Louis de Carcassonne, Grenade sur Garonne .....
- Là se retrouve, de façon
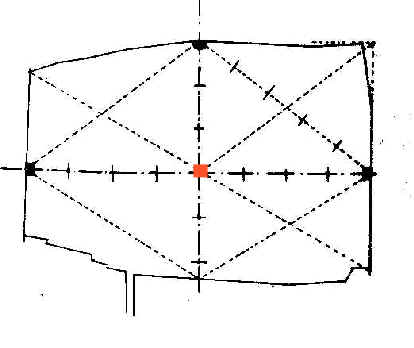
évidente, l'usage de La corde à 12 intervalles ou 13 noeuds
pour appliquer le triangle de Pythagore. En effet, partout présent, le
triangle de Pythagore répartit l'espace dans une proportion 3 / 4, sans
oublier l'enceinte, la longueur des rues principales ( dont
l'intersection marque le centre de la bastide ) avant les moulons
(quartiers) et la place (qui n'est pas exactement le centre de la
bastide).
- Monpazier
|
|
|

|
|

|
- .
- L'étude du plan de Villeneuve sur
Lot confirme la démarche adoptée à Monpazier. En entrant dans le détail,
il est loisible de constater que les moulons (quartiers) et les parcelles
individuelles sont dessinés sur une base de référence identique c'est à
dire le triangle de Pythagore.
- Villeneuve sur lot
|
|

|
- .
- Cette application du triangle de Pythagore,
comme l'a signalé Lavedan, atteint son extrême limite théorique avec
Monflanquin dont la topographie aurait dû entraîner une solution pratique
prenant en compte les courbes de niveau. Mais le schéma classique a été
appliqué sans concession à la réalité topographique et l'un des coins de
la place marque très normalement le centre du tracé de la bastide.
- .
- II/ Plan
Théorique modifié :
-
- Cependant, le plus grand nombre de bastides
ont, d'une façon ou de l'autre, transigé avec ce schéma théorique
classique.
- Vianne, par exemple, s'inscrit bien dans le
schéma, mais le modifie légèrement, dans sa partie Est, pour englober le
moulin et le port préexistant sur la Baïse. Légère modification
également pour englober l'église Notre Dame vestige de l'ancien village de
Villelongue précédant la construction de la bastide. D'ailleurs l'église
est oblique par rapport au parcellaire.
.
A Castillonnès, autre exemple, le
gauchissement du plan classique va très loin et prouve que l'adaptation
peut à la fois tenir compte de la topographie et de la récupération d'un
castrum antérieur.
- Castillonnes
|
|
 |
- .
- III/ Typologie de
Plans de bastides :
- Il y a donc eu des adaptations et des
variantes de solutions à partir d'un même canevas reposant sur le triangle
de Pythagore. Souvent ces variantes ont été très proches au sein d'une
même région soit par l'exemplarité de l'une des bastides initiant
localement le processus, soit sous l'influence d'un même traceur
itinérant. Ce qui permet un essai de typologie.
- Cet essai de typologie -
voir
le détail dans "caractéristiques
: 4/ Essai deTypologie" - est aléatoire comme,
souvent, toute modélisation (réductrice par nature). Elle n'est donc
proposée qu'à condition de la dépasser en abordant chacune des bastides
étudiées.
- Selon le site
Géographique
|
- Bastide de hauteur
|
-
|
- Bastide
de Rivière
|
|
-
|

|
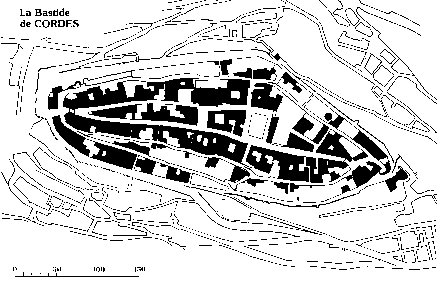
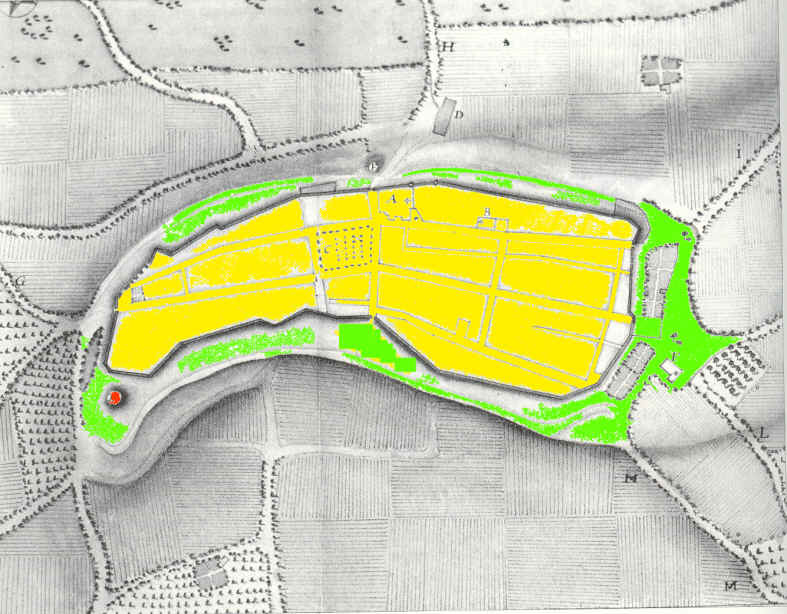
- Cordes
|
-
|
- Villefranche
Rouergue
|
- .
- Selon un modèle
|
- Modèle Quercynois
|
-
|
- Modèle Aquitain
|
|
-
|

|
- Le Plan
|
-
|
- Monpazier
|
-
|
- Modèle Gimontois
|
-
|
- Modèle Gascon
|

|
-
|

|
- Gimont
|
-
|
- Mirande
|
- .
- .
- "La corde à
12 noeuds"
- dîte aussi
- "la corde à 13 noeuds"
|
-

- Pourquoi l’appelle-t-on «corde à 1
2 nœuds» ?
La corde à 12 nœuds est une corde comportant 12
intervalles égaux, ce qui fait donc bien 12 noeuds si l'on n'a pas fait de nœud
au début de la corde.
Mais
il y a13 nœuds si l'on en
fait un à chaque extrémité (toujours pour 12 intervalles).
-
Un intervalle correspond à une coudée.
Donc 12 intervalles = 630, 72 cm.(dans
le cas ici choisi, mais variable selon les régions)
- A
quoi sert la corde à 12 nœuds ?
.
- La
corde à 12 nœuds sert notamment à reporter au sol les tracés exactes des
figures géométriques. Cet outil permet notamment de tracer des angles droits,
des triangles isocèles, des droites perpendiculaires… et tout cela sans
utiliser d’unités de mesure algébriques.
-
S
La corde à 12 noeuds
-
S
Que dit le théorème de Pythagore ?
|
-
.
- * *
- *
- Bibliographie
- - "Le bâti ancien en bastide" Calmettes et Cornu
- 1985
- - "Bastides, villes nouvelles du moyen-âge"
Lauret A., Malebranche R., Séraphin G. - éd. Milan 1992
- - "Les bastides, essai sur la régularité"
Divorne F. Gendre B. Lavergne B. Panerai P. -éd. AAM 1985.
- - "La bastide de Monpazier" Pons J.- 1997.
- - "Castillonnés" Hoare L. - CEB
1990.
- - "Vianne" Higounet Ch. - CEB 1984.
- Cartes CEB |